11. Bodies and Shapes
11.1. RigidBody
An agx::RigidBody is an entity in 3D space with physical properties such as mass and inertia tensor and dynamic properties such as position, orientation and velocity.
A rigid body is created as follows:
agx::RigidBodyRef body = new agx::RigidBody();
simulation->add( body ); // Add body to the simulation
There are three motion control schemes for a RigidBody:
DYNAMICS |
Affected by forces, position/velocity is integrated by the DynamicsSystem. |
STATIC |
Not affected by forces, considered to have infinite mass, will not be affected by the integrator. |
KINEMATICS |
Controlled by the user. By supplying a target transformation and a delta time, a linear and an angular velocity are calculated. This velocity will be used by DynamicsSystem to interpolate the position/orientation of the kinematic RigidBody. The angular velocity is considered to be constant during the interpolation. |
The type of motion control is set with the method:
RigidBody::setMotionControl(RigidBody::MotionControl);
11.1.1. Velocities
The angular and linear velocity of a rigid body is always understood as the velocity of the center of mass. Velocities of a rigid body are expressed in the world coordinate system.
agx::Vec3 worldVelocity(0,1,0);
// Specify the linear velocity in world coordinates for a rigid body
body->setVelocity( worldVelocity );
// Specify angular velocity for a body in LOCAL coordinate system
agx::Vec3 localAngular(0,0,1);
// Convert from local to world coordinate system
agx::Vec3 worldAngular = body->getFrame()->transformVectorToWorld( localAngular);
// Set the angular velocity in World coordinates
body->setAngularVelocity( worldAngular );
11.2. Velocity damping
AGX has a damping term (angular and linear) one for each coordinate axis (in the body’s local coordinate system). It can be specified through the API as:
rigidBody->setLinearVelocityDamping( const Vec3f& damping );
rigidBody->setAngularVelocityDamping( const Vec3f& damping );
With this damping term D and the gravitational mass m, we will get a new mass matrix M’ such that:
Analogous for the moment of inertia tensor.
Now given this effective mass matrix M’ and the original mass matrix M we get the velocity integration equation:
This means that if damping > 0, the term \(M' M\) will be < 0 and the velocity will be damped with a viscous damping term. The effective mass (including damping) will enter the system of equation on the left side, illustrated in the simplified linearized stepping equation below:
For a more complete description see equation 4.31 in [2].
11.3. Effective Mass
When for example simulating a ship in water, the effective mass can be substantially larger than the actual weight of the ship.
This is due to the water that is added by hydrodynamic effects. The mass varies depending on depth of water and is also different in different directions.
The class agx::MassProperties has the capability of handling this added mass through the methods:
void setMassCoefficients( const Vec3& coefficients );
void setInertiaTensorCoefficients(const Vec3& coefficients);
This also means that AGX can handle objects that have different masses along each axis, so called non-symmetric mass matrices.
11.4. Modelling coordinates/Center of Mass coordinates
Center of mass is the point in the world coordinate system where the collected mass of a rigid body is located in space. This point can either automatically be calculated from the geometries/shapes that are associated to the rigid body, or it can also be explicitly specified to any point in space.
Since the center of mass moves when geometries are added (if RigidBody::getMassProperties()::getAutoGenerate()==true), it is not a practical reference when building a simulation.
For example, if a constraint is attached to a body relative to the body center of mass, adding another geometry and thereby moving the center of mass would change to attachment point for the constraint.
This is usually not the expected/wanted behavior.
Therefore AGX provides two coordinate frames, the model frame and the center of mass(CM) frame.
Fig. 11.1: shows one box with the model origin (axes) and the center of mass (yellow sphere) at the same positions. Fig. 11.2: illustrates the situation after another box geometry is added to the body, and thus the center of mass (yellow sphere) is shifted along the y-axis. The model origin (axes) is still at the same position.
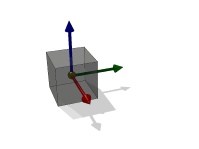
Fig. 11.1 Model and Center of mass at the same position.
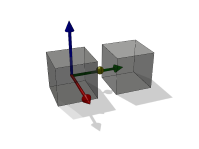
Fig. 11.2 Center of mass translated due to added geometry.
Note
AGX only supports relative translation of the center-of-mass-frame with regard to the model frame, but not relative rotation.
The translation, rotation and velocity of the center of mass for a rigid body can be accessed via the methods:
agx::RigidBodyRef body = new agx::RigidBody;
// Get position of Center of Mass in world coordinate system
Vec3 pos = body->getCmPosition();
// Get orientation of Center of Mass in world coordinate system
Quat rot = body->getCmRotation();
// Get rotation and translation of Center of Mass in world
// coordinate system
AffineMatrix4x4 m = body->getCmTransform();
// Or the complete frame at one call
Frame *cmFrame = body->getCmFrame();
// Translation relative to model coordinate system
Vec3 pos = body->getCmFrame()->getLocalTranslate();
// In most situation, it is the model coordinate system that is interesting. This can be accessed using the calls:
// Get position of Rigid Body in world coordinate system
Vec3 pos = body->getPosition();
// Get orientation of Rigid Body in world coordinate system
Quat rot = body->getRotation();
// Get rotation and translation of Rigid Body in world coordinate system
AffineMatrix4x4 m = body->getTransform();
// Or the complete frame at one call
Frame *cmFrame = body->getFrame();
// Get linear velocity of body
Vec3 v = body->getVelocity()
/**
\return the local offset of the center of mass position to the model origin (in model frame coordinates).
*/
agx::Vec3 getCmLocalTranslate() const;
/**
Sets the local offset of the center of mass position to the model origin (in model frame coordinates).
\param translate The new offset.
*/
void setCmLocalTranslate(const agx::Vec3& translate);
11.5. Kinematic rigid body
By specifying that a rigid body should be kinematic, we are telling the DynamicsSystem to stop simulating the dynamics of the body. This means that it will get an infinite mass, will not be affected by forces etc.
rigidbody->setMotionControl( agx::RigidBody::KINEMATICS );
It is also possible to interpolate the position/orientation based on a target transformation specified by the user. The body can then be specified to move from the current transform to a new during a specified time step with the call to:
agx::RigidBody::moveTo(AffineMatrix4x4& transform, agx::Real dt);
The above method will make a body move in a velocity calculated from its current transformation frame, to the specified during a time interval of dt.
When the interval dt is reached (current time + dt) the body will continue to move according to its velocity until next call to moveTo().
If you explicitly set a linear/angular velocity on a body, and specify it to be KINEMATICS, then that velocity will be used for integrating the transformation (position and orientation).
11.6. Geometry
A Geometry can be assigned to a rigid body to give it a geometrical representation. The geometry is also the entity that can intersect other geometries and create contacts. A Geometry contains one or more shapes. A Shape is specialized by Box, Sphere, Capsule etc. see table 11.4 for a complete list of available shapes.
11.6.1. Enable/disable
A Geometry can be enabled/disabled. A disabled geometry will not be able to collide with any other geometries. This is true for all the shapes in the geometry. A disabled geometry will not contribute to the mass properties of a rigid body.
void Geometry::setEnable( bool enable );
bool Geometry::getEnable() const;
bool Geometry::isEnabled() const;
Calling geometry->setEnable(false) will effectively remove the geometry from the mass calculation and collision detection.
11.6.2. Mass property calculations
A Geometry can also be disabled for mass property calculation. This means that it can still collide, but will not contribute to the mass properties of a rigidbody.
agx::RigidBodyRef body = new agx::RigidBody();
agxCollide::Geometry sphere1 = new agxCollide::Geometry(new agxCollide::Sphere(0.5));
agxCollide::Geometry sphere2 = new agxCollide::Geometry(new agxCollide::Sphere(0.5));
// This sphere will not be part of the mass property calculation for the rigid body
sphere2->setEnableMassProperties(false);
body->add(sphere1);
body->add(sphere2, agx::AffineMatrix4x4::translate(-1, 0, 0));
// Mass will still be the mass of one sphere.
// Same for Inertia
// cm_translate will be (0, 0, 0)
auto cm_translate = body->getCmLocalTranslate();
// Enable the second sphere for mass property calculation
sphere2->setEnableMassProperties(true);
// Update the mass propertices for the rigidbody
// Mass will now be 2x the mass of one sphere.
// Inertia and cm will also be updated
body->updateMassProperties();
11.6.3. Sensors
A geometry can be specified to be a sensor. This means that the collision system will generate contact information, such as contact points, normals and penetration, but no physical contact (contact constraint) will be created, hence the solver will not see this contact. A sensor can therefore penetrate any other geometry as a “ghost”. This can be useful for realizing certain functionality such as proxy tests, vision etc. A geometry is specified to be a sensor through the call:
agxCollide::GeometryRef geometry = new agxCollide::Geometry;
geometry->setSensor( true ); // Tell the geometry to become a Sensor
A sensor geometry will not add any physical properties such as mass, center of mass, or inertia tensor to the body it is part of. Calling setSensor(true) will effectively remove the geometry from the mass calculation.
In some cases it is enough to know that a sensor overlapped with some other geometry, without any need for the contact point data. Performance can be improved by not computing that data and instead letting the collider do an early out as soon as possible when an overlap has been detected. Contact data generation is disabled for a sensor geometry by passing false as the second argument to setSensor:
geometry->setSensor(true, false);
Disabling contact generation on a geometry that isn’t a sensor has no effect, contact points will always be generated for geometries that aren’t sensors.
Support for collider early out is added on a shape-type-pair basis and not all pairs are handled yet. Currently supported are:
box-trimesh
cylinder-trimesh
sphere-trimesh
11.7. Enabling/disabling Contacts
There are several different alternatives to control whether pairwise contacts should occur or not.
It should be noted that there is not direct priority between these different possibilities, but rather, if any of them disables the contact (even if others enable it), the contact generation will be treated as disabled.
11.7.1. Disable collisions for a geometry
To explicitly disable all collision generation for a geometry:
// Disable all contact generation for the geometry:
geometry1->setEnableCollisions( false );
11.7.2. Enable/disable pair
To disable/enable contacts for a specific geometry pair one can call the method Geometry::setEnableCollisions( Geometry*, bool )
// Disable contact generation between geometry1 and geometry2
geometry1->setEnableCollisions( geometry2, false );
// Enable contact generation between geometry1 and geometry2
geometry1->setEnableCollisions( geometry2, true );
The state regarding geometries being disabled/enabled for collision against each other will be stored in the geometries. So removing/adding them from/to a simulation, the result will still be the same.
11.7.3. GroupID
The class Geometry has a groupID attribute. This attribute can be set and read using the following methods:
void agxCollide::Geometry::addGroup( unsigned );
bool agxCollide::Geometry::hasGroup( unsigned ) const;
bool agxCollide::Geometry::removeGroup( unsigned );
With the method addGroup() one can assign a geometry to a specified group of geometries.
Together with the following method in agxCollide::Space:
void agxCollide::Space::setEnablePair(unsigned id1,
unsigned id2,
bool enable)
This functionality can be used to disable collisions between groups of geometries. To disable collisions between geometries of the same group:
space->setEnablePair( id1, id1, false );
After the above call, geometries belonging to id1 cannot collide with each other. t is worth to notice that the group ids are stored in a vector, so searching and comparing has a time complexity of O(n). So before adding a large number of group ids to a geometry, make sure there isn’t another alternative. This is because the geometry groups will be compared to each other during the collision detection process.
11.7.4. Named collision groups
New in 2.3.0.0 is that there is also named collision groups. This has the same functionality as GroupID, but it is defined using a string instead.
void agxCollide::Geometry::addGroup( const agx::Name& );
bool agxCollide::Geometry::hasGroup(const agx::Name& ) const;
bool agxCollide::Geometry::removeGroup(const agx::Name& );
This functionality can be used to disable collisions between groups of geometries. To disable collisions between geometries of the same group:
space->setEnablePair( name1, name1, false );
After the above call, geometries belonging to name1 cannot collide with each other.
11.7.5. User supplied contact listener
A ContactEventListener (see 10.4.3) can be registered to listen to specific collision events, between specified geometries, geometries with specific properties etc. By implementing a collision event listener that for a given pair of geometries return REMOVE_CONTACT or KEEP_CONTACT immediately in the impact() method, one can achieve the same result as the previous two alternatives, namely, no contact is transferred to the contact solver. This is a very general way of specifying for which pairs contacts should be generated.
class MyContactListener : public agxSDK::ContactEventListener
{
public:
MyContactListener()
{
// Only activate upon impact event
setMask(agxSDK::ContactEventListener::IMPACT);
}
bool impact(const agx::TimeStamp& t, agxCollide::GeometryContact *cd) {
RigidBody* rb1 = cd->geomA->getBody();
RigidBody* rb2 = cd->geomB->getBody();
// If both geometries have a body, and the mass of the first is over 10
// then remove the contact
if (rb1 && rb2 && rb1->getMassProperties()->getMass() > 10 )
return REMOVE_CONTACT; // remove contact.
return KEEP_CONTACT; // keep the contact
}
};
Which geometries should trigger the ContactEventListener can be specified using an ExecuteFilter. This filter can also be user specified. By deriving from the class agxCollide::ExecuteFilter and implementing two methods, any user supplied functionality can be implemented for filtering out contacts:
class MyFilter : public agxCollide::ExecuteFilter
{
public:
MyFilter() {}
/**
Called when narrow phase tests have determined overlap (when we have
detailed intersection between the actual geometries).
Return true if GeometryContact matches this filter:
if both geometries have a body.
*/
virtual bool operator==(const agxCollide::GeometryContact& cd) const
{
bool f =
(cd.geomA->getBody() && cd.geomB->getBody());
return f;
}
/**
Called when broad phase tests have determined overlap between the two
bounding volumes.
*/
virtual bool operator==(const GeometryPair& geometryPair) const
{
bool f =
(cd.geomA->getBody() && cd.geomB->getBody());
return f;
}
};
11.7.6. Surface velocity
A geometry can be given a surface velocity. It is specified in the local coordinate system of the geometry and can be used for simulating the surface of a conveyor belt. In its general form, it is independent of the contact point position relative to the geometry. If more control over that behavior is desired, it is possible to create a class inheriting from agxCollide::Geometry, and to override the method
agx::Vec3f Geometry::calculateSurfaceVelocity( const agxCollide::LocalContactPoint& point ) const.
One such class is agx::SurfaceVelocityConveyorBelt, which is described in Section 33.
11.8. Primitives for collision detection (Shapes)
AGX allows for different shapes for geometric representation. Simpler shapes such as Box, Sphere or Cylinder allow for exact representation of simple geometry, as well as fast compute times.
Mesh types such as Trimesh, Convex or HeightField allow for more complex geometry, at the cost of higher compute times.
11.8.1. Box
A box is defined by three half extents with its center of mass at origin.
Box::Box( const agx::Vec3& halfExtents )
11.8.2. Sphere
A sphere is defined by its radius and is created with its center of mass at origin.
Sphere::Sphere( const agx::Real& radius )
11.8.3. Capsule
A capsule is a cylinder, capped with two spheres at the end. It is defined by its height and its radius. The capsule will be created with its height along the y-axis and its center of mass at origin.
Capsule::Capsule( agx::Real radius, agx::Real height )
11.8.4. Cylinder
Cylinder::Cylinder( const agx::Real& radius, const agx::Real& height )
11.8.5. HollowCylinder
A hollow cylinder is similar to a cylinder but with a circular hole.
HollowCylinder::HollowCylinder( agx::Real innerRadius, agx::Real height, agx:Real thickness )
This shape is suitable for modeling peg-in-a-hole kind of scenarios in combination with other cylinders, hollowcylinders or different kinds of cones.
Note
A current limitation is that the hollow cylinder does not have full collision support against all other shape types. Until full support is available according to table 11.4, a fallback is used which treats the HollowCylinder as a Cylinder.
To give an example, the pair HollowCylinder - Sphere does not have full support and hence the sphere can not be sent through the hollow part of the cylinder due to the hollow cylinder being treated as a cylinder shape.
11.8.6. Line
A line is defined by two points, begin and end points:
Line::Line( const agx::Vec3& start, const agx::Vec3& end )
11.8.7. Plane
A plane can be defined in a number of different ways: either by a point and a normal, or the four plane coefficients:
Plane::Plane( agx::Real const a, agx::Real const b,
agx::Real const c, agx::Real d )
Plane::Plane( const agx::Vec3& normal , agx::Real d )
Plane::Plane( const agx::Vec3& normal, const agx::Vec3& point )
Plane::Plane( const agx::Vec4& plane)
Plane::Plane( const agx::Vec3& p1, const agx::Vec3& p2,
const agx::Vec3& p3)
11.8.8. Cone / HollowCone
Cone::Cone( agx::Real topRadius, agx::Real bottomRadius, agx::Real height )
HollowCone::HollowCone( agx::Real topRadius, agx::Real bottomRadius, agx::Real height, agx::Real thickness )
A Cone and a HollowCone are very similar. The main difference is that the hollow cone has a conical hole. Both cone types support a non-zero topRadius which creates a truncated cone where the top part is cut off.
The cones are defined alony the Y-axis and the bottom disc is positioned at y=0 and the top point (or top disc in case of truncation) is placed at y=height.
Note
HollowCone and Cone does not currently support all other shapes. Until each collider is implemented to take into account the actual cone shape, a fallback treating them as a Convex will be used. See table 11.4.
11.8.9. Triangle mesh
11.8.9.1. Triangle mesh construction
The triangle mesh shape in AGX supports general concave triangle meshes.
The internal storage of triangle meshes in AGX is based on vertices (array of 3D points) and indices (indexes into the array of vertices), where three concurrent indices define a triangle each (a triangle list).
Trimeshes share a common base class called agxCollide::Mesh with another mesh-based collision shape called agxCollide::HeightField.
A trimesh can be created using code or by reading from a support mesh file format (see Mesh reader). Below is an example of how a trimesh can be created from code or from a file
agx::Vec3Vector vertices;
agx::UIntVector indices;
// Add vertices
vertices.push_back( agx::Vec3( -0.4, -0.4, 0.0 ) );
// ...
// Add indices
indices.push_back( 1 ); // starting first triangle
indices.push_back( 0 );
indices.push_back( 2 ); // finished first triangle
indices.push_back( 0 ); // starting second triangle, reusing one vertex
// ...
// Create the collision shape based on the vertices and indices
agxCollide::TrimeshRef triangleMesh = new agxCollide::Trimesh( &vertices,
&indices, "handmade pyramid" );
And from a file:
// Create the trimesh shape from a WaveFront OBJ file:
agxCollide::TrimeshRef trimeshShape =
agxUtil::TrimeshReaderWriter::createTrimesh(
"torusRoundForCollision.obj");
The data will be copied by the trimesh constructor.
Furthermore, the triangles are expected to be given in counterclockwise order (counterclockwise winding/orientation).
This is important since the order of the vertices defines which face of the triangle will point outwards and which inwards.
This orientation is used within calculation of mass properties and collision detection.
If the data is given in clockwise winding, this can be indicated by setting the according flag in agxCollide::Trimesh::TrimeshOptionsFlags.
Mixed winding should be avoided since it will lead to unexpected behavior.
The flag agxCollide::Trimesh::RECALCULATE_NORMALS_GIVEN_FIRST_TRIANGLE can be used to adapt the winding to the first triangle, given that the mesh is watertight otherwise.
Internally, the triangle data will be stored in counterclockwise winding.
For good collision detection results, each trimesh should be a watertight (a geometrical manifold). Non-manifold trimeshes can be used, but the results may vary in quality. Non-manifold trimeshes may furthermore result in an invalid mass and inertia when used in dynamic rigid bodies for which mass properties are calculated automatically.
11.8.9.2. Triangle meshes as terrain
Trimeshes can also be used to model terrains. Here, they do not have to be closed on all sides, but may have an open direction. This direction is assumed to be upward in z direction in the trimesh’s local coordinate system. The corresponding normal (0, 0, 1) is used as a tunneling safeguard, and the trimesh’s bounding box is enlarged in opposite direction of this normal by a value called the terrain’s “bottom margin”.
It is recommended to avoid collisions at terrain borders unless they are met by a corresponding neighboring terrain, since this might give suboptimal results. The trimesh class will give out warnings during construction if a terrain does not have a rectangular shape (in the trimesh’s local x and y coordinates), or contain holes. The usage as terrain should be indicated in the optionsMask.
One example for a terrain with a bottom margin of 5.0 below the mesh’s deepest point in Z:
agx::Vec3Vector vertices;
agx::UIntVector indices;
// Add vertices
vertices.push_back( agx::Vec3( -0.4, -0.4, 0.0 ) );
...
// Add indices
indices.push_back( 1 ); // starting first triangle
uint32_t optionsMask = agxCollide::Trimesh::TERRAIN;
...
TrimeshRef terrain = new Trimesh( &vertices, &indices, "handmade terrain", optionsMask, 5.0 );
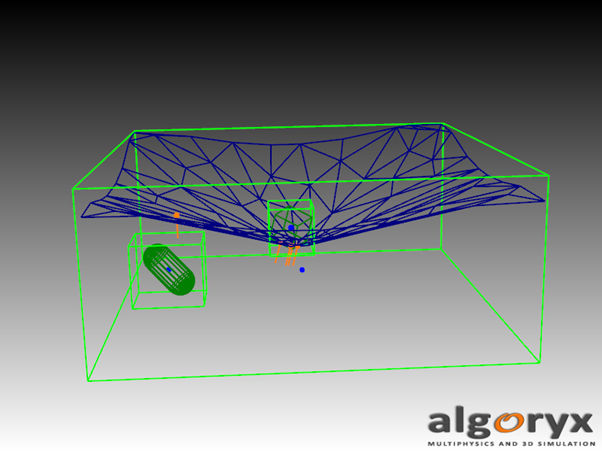
Fig. 11.3 Terrain/trimesh intersecting a box, and a capsule which is prevented from tunneling. Note the enlarged bounding box in opposite direction of the terrain normal.
Using a height-field for collision detection as a terrain has the advantage of being able to modify the terrain during run-time. Trimeshes as terrains, on the other hand, can be modeled with fewer triangles by adapting the level of detail to the local change in terrain height, so that large plain parts can be covered by few large triangles.
11.8.9.3. Triangle meshes modeling
As mentioned above, special attention should be paid when using triangle meshes as collision primitives.
It is important that the models are adapted for the special needs arising from physics simulation, and thus are either manifolds or used as terrain.
Potential problems (which should be fixed externally before using the trimesh) are:
Unmerged identical vertices
Holes
Wrong/inconsistent winding
Triangles with zero area
Unreferenced vertices
Self-intersection.
Trimeshes used in collision detection create potentially very many contact points. The use of contact reduction is therefore recommended.
The meshes in AGX normally have a half-edge structure. See further in Triangle mesh traversal. If the half-edge structure has edges with no neighbor, then it can be a sign of one or more of the problems listed above. As a help, there is a python utility which can be used to visualize missing half-edges.
It is either used with python such as python data/python/trimesh-visualization.py path/to/mesh.obj
or used in combination with e.g. agxViewer by using --attachScript data/python/trimesh-visualization.py.
The script will look for all trimeshes in the simulation, check for edges with no
half-edge neighbor and debug-render these in red.

Fig. 11.4 Example visualization of a loaded trimesh where there are some regions which do not have neighbor half-edges.
11.8.9.4. Mesh reduction
The time for computing geometry contacts when using a triangle mesh model can be related to the complexity of the triangle mesh. I.e. the number of triangles.
agxUtil::reduceMesh is a function that can reduce the complexity of a triangle mesh by algorithmically reduce the number of edges in a process called collapsing.
The goal of the mesh reduction is to reduce the number of triangles but at the same time keep the overall shape of the mesh.
The function operates on arrays of vertices and indices to be as general as possible. Below is a code snippet that demonstrates the functionality of the mesh reduction utility. The arguments are the set of vertices and indices that should be reduced, the target reduction (in percent, 1==no reduction, 0.5==50% reduction) and an aggressiveness (>0). The higher value, the more aggressive the algorithm will be, and the longer time it will take.
agxIO::MeshReaderRef reader = new agxIO::MeshReader();
reader->readFile("data/models/bunny.obj");
agx::Vec3Vector out_vertices;
agx::UInt32Vector out_indices;
double target_reduction = 0.5; // % triangles that should be left in the model after reduction
double aggressiveness = 7.0; // A value that indicates how aggressive the reduction should be
agxUtil::reduceMesh(reader->getVertices(), reader->getIndices(),
out_vertices, out_indices,
target_reduction,
aggressiveness);
// Create a Trimesh with the reduced data
agxCollide::TrimeshRef mesh = new agxCollide::Trimesh(&out_vertices, &out_indices,
"Mesh",
agxCollide::Trimesh::REMOVE_DUPLICATE_VERTICES);
11.8.9.5. Triangle mesh traversal
If a trimesh is modeled in the above recommended way and thus has a half edge structure, it can be traversed via this neighborhood graph: each triangle consists of three half edges, where each half edge has a neighboring half edge in a bordering triangle, and where one half edge’s starting vertex is the other one’s ending vertex.
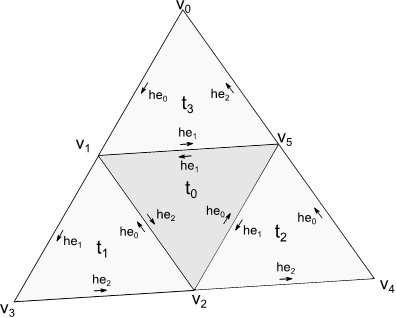
Fig. 11.5 A trimesh consisting of 4 triangles and 6 vertices. The half edge structure is shown.
This data is stored as arrays of vertices, triangle half edges and half edge neighbors in the Trimesh class and can be used directly.
Some helper classes make traversal of triangles easier, though. The neighborhood structure can be traversed by using the helper class agxCollide::Mesh::Triangle.
// Create the trimesh shape from a WaveFront OBJ file:
agxCollide::TrimeshRef trimesh =
agxUtil::TrimeshReaderWriter::createTrimesh( "pin.obj" );
// Get first triangle in trimesh
agxCollide::Mesh::Triangle triangle = trimesh->getTriangle(0);
if (triangle.isValid()) // Important to check validity before use
triangle = triangle.getHalfEdgePartner(0); // Get neighbor to first edge
Circling around a vertex can be done more comfortably using the helper class agxCollide::Mesh::VertexEdgeCirculator.
// Create the trimesh shape from a WaveFront OBJ file:
agxCollide::TrimeshRef trimesh =
agxUtil::TrimeshReaderWriter::createTrimesh( "pin.obj" );
// Get a circulator around the first vertex in the first triangle.
agxCollide::Mesh::VertexEdgeCirculator circulator =
trimesh->createVertexEdgeCirculator( 0, 0 );
// The circulator might be invalid if created from invalid parameters.
if (circulator.isValid()) {
// Has the circulator done a whole turn around the vertex?
while (!circulator.atEnd()) {
// Set it to next position. The VertexEdgeIterator will even manage
// holes in the neighborhood structure by jumping over all holes.
circulator++;
if (circulator.hasJustJumpedOverHole())//Have holes been passed?
std::cout << "Vertex circulator jumped over hole\n";
}
}
More elaborate examples can be found in tutorial_trimesh.cpp.
11.8.10. Convex
Convex is a geometry that describes a convex shape built up from a point cloud. The properties of a convex is among the following: none of the surface normals of a convex will ever cross each other, any point on a 2D projection of a convex will only be covered twice, once from the surface facing away the projection plane and once from the surface facing the projection plane.
A convex mesh can be created from a number of different sources.
From a triangle mesh that is known to define a convex mesh.
From a set of 3d points.
From 3d mesh files.
Using convex decomposition of triangle meshes.
If you have mesh data (vertices and indices) that you _know_ are convex, you can use the constructor to create a convex mesh:
agx::Vec3Vector vertices;
agx::UIntVector indices;
// We know this data to represent a convex mesh:
ConvexRef convex = new Convex(&vertices, &indices);
If you have a set of 3d points you can use the utility function in the agxUtil::ConvexReaderWriter namespace:
#include <agxUtil/ConvexReaderWriter/ConvexReaderWriter>
agx::Vec3Vector vertices;
for(size_t i=0; i < 30; i++)
{
auto v = agx::Vec3::random( agx::Vec3(0, 0, 0), agx::Vec3(1, 1, 1) );
vertices.push_back(v);
}
// Create the collision shape
agxCollide::ConvexRef convexMesh = agxUtil::ConvexReaderWriter::createConvex(vertices);
If you have a 3d mesh defined in a file:
#include <agxUtil/ConvexReaderWriter/ConvexReaderWriter>
// Create the collision shape
agxCollide::ConvexRef convexMesh = agxUtil::ConvexReaderWriter::createConvex("models/bunny.obj");
11.8.10.1. Convex decomposition

Fig. 11.6 A triangle mesh object decomposed into convex meshes with varying resolution.
The limitation of convex in that it can only describe a small subset of geometries (convex) can be overcome by taking a general (concave) triangle mesh and decompose it into convex meshes.
The result will not be an exact representation of the original triangle mesh, but in many cases it will be good enough for use in simulations.
AGX supports convex decomposition through the class agxCollide::ConvexFactory where you have full control over the parameterization of the algorithm.
#include <agxCollide/ConvexFactory.h>
// Create a ConvexFactory
agxCollide::ConvexFactoryRef factory = new agxCollide::ConvexFactory;
// Create a mesh reader for various mesh file formats.
agxIO::MeshReaderRef reader = new agxIO::MeshReader;
if (!reader->readFile( "mesh.obj"))
error();
// Create a parameter object so we can fine tune the decomposition algorithm:
agxCollide::ConvexFactory::VHACDParametersRef parameters = new agxCollide::ConvexFactory::VHACDParameters();
parameters->resolution = 20;
parameters->alpha = 0.001;
parameters->beta = 0.01;
parameters->concavity = 0.01;
parameters->maxNumVerticesPerCH = 64
// Try to parse the data read from the reader and create convex shapes
size_t numConvexShapes = factory->build(reader, parameters);
if (numConvexShapes == 0)
error();
// Get the vector of the created shapes
agxCollide::ConvexShapeVector& shapes = factory->getConvexShapes();
// Now insert shapes into one or more geometries.
An alternative is to use simpler utility function agxUtil::ConvexReaderWriter::createConvexDecomposition:
#include <agxUtil/ConvexReaderWriter/ConvexReaderWriter.h>
size_t resolution = 20;
agxCollide::ConvexShapeVector shapes
agxUtil::ConvexReaderWriter::createConvexDecomposition("mesh.obj", result, resolution);
// Now insert shapes into one or more geometries.
Below are the available parameters to the convex decomposition algorithm.
Parameter |
Description |
Range |
Default value |
|---|---|---|---|
resolution |
maximum number of voxels generated during the voxelization stage. This will be recalculated as resolution ^3 before it reaches VHACD |
[2, 400] |
50 |
concavity |
maximum concavity. |
[0.0, 1.0] |
0.0025 |
planeDownsampling |
Controls the granularity of the search for the best clipping plane. |
[1, 16] |
4 |
convexhullDownsampling |
Controls the precision of the convex-hull generation process during the clipping plane selection stage. |
[1, 16] |
4 |
alpha |
Controls the bias toward clipping along symmetry planes. |
[0.0, 1.0] |
0.05 |
beta |
Controls the bias toward clipping along revolution axes. |
[0.0, 1.0] |
0.05 |
pca |
Enable/disable normalizing the mesh before applying the convex decomposition. |
[false, true] |
0 |
mode |
0: voxel-based approximate convex decomposition, 1: tetrahedron-based approximate convex decomposition. |
0/1 |
0 |
maxNumVerticesPerConvex |
Controls the maximum number of triangles per convex hull. |
[0, 1024] |
64 |
minVolumePerConvex |
Controls the adaptive sampling of the generated convex hulls. |
[0.0, 0.01] |
0.0001 |
maxConvexHulls |
Maximum number of convex hulls. |
[1, 1024] |
1024 |
11.8.11. Oriented bounding volumes
Oriented Bounding Volumes (OBV) (box, cylinder, capsule) can be computed based on a set of vertices. An optimal OBV should tightly enclose the vertices to best represent the more complex shape.
Below is a code snippet that will create an oriented Box shape that will fit the given vertices. The size and the transformation are stored in the supplied arguments to agxUtil::computeOrientedBox.
The transformation will contain the translation and rotation of the box relative to the coordinate system of the vertices (mesh).
// Get the vertices from an existing mesh shape
const agx::Vec3Vector& vertices = mesh->getMeshData().getVertices();
// Here is where we will store the local transformation of the oriented box relative to the Mesh
agx::AffineMatrix4x4 transform;
// Here is where we will store the size of the computed oriented box
auto halfExtents = agx::Vec3();
// Compute the size and rotation of the oriented box given the vertices
agxVerify(agxUtil::computeOrientedBox(vertices, halfExtents, transform));
// Create a box primitive based on the computed size
auto box = new agxCollide::Box(halfExtents);
// Create a Geometry including the transform that will rotate/translate the oriented bounding box relative to the mesh
auto boxGeometry = new agxCollide::Geometry(box, transform);
Alternatively an oriented Cylinder or Capsule can be created using agxUtil::computeOrientedCylinder and agxUtil::computeOrientedCapsule
There is an option on how the shape should be oriented using the enum agxUtil::ShapeOrientation::Orientation. Default is agxUtil::ShapeOrientation::MINIMIZE_VOLUME which will automatically choose the principal axis of the computed shape that results in the smallest volume.
Below is code that will create an oriented cylinder based on a set of vertices.
// Get the vertices from an existing mesh shape
const agx::Vec3Vector& vertices = mesh->getMeshData()->getVertices();
// Here is where we will store the local transformation of the oriented box relative to the Mesh
agx::AffineMatrix4x4 transform;
// Here is where we will store the radius and height of the computed cylinder
auto radiusHeight = agx::Vec2();
auto orientation = agxUtil::ShapeOrientation::MINIMIZE_VOLUME; // Default
// Compute the size and rotation of the oriented box given the vertices
agxVerify(agxUtil::computeOrientedCylinder(vertices, radiusHeight, transform, orientation));
// Create a cylinder primitive based on the computed size
auto cylinder = new agxCollide::Cylinder(radiusHeight[0], radiusHeight[1]);
// Create a Geometry including the transform that will rotate/translate the oriented bounding cylinder relative to the mesh
auto boxGeometry = new agxCollide::Geometry(cylinder, transform);

Fig. 11.7 This figure show a number of alternative bounding volumes and selection of principal axis for the computed shape.
11.8.12. WireShape
The wire shape is used internally for the collision handling of wire segments. It is based on the capsule, but might in the future have support for continuous collision detection. It is not advised to use this shape for other purposes, since implementation details might change.
11.8.13. HeightField
A height field is a geometric representation that can be used for terrain, sea beds etc.
Height-fields are currently implemented as a scaled uniform grid centered at the local origin in x and y, and with z up.
Furthermore, height-fields are treated like triangle meshes, where each rectangular grid cell is divided into a lower left and an upper right triangle.
The corresponding class agxCollide::HeightField shares a common base class called agxCollide::Mesh with another mesh-based collision shape called agxCollide::Trimesh.
Compared to a trimesh, a height-field for collision detection as a terrain has the advantage of being able to modify the terrain under run-time. Trimeshes as terrains, on the other hand, can be modeled with fewer triangles by adapting the level of detail to the local change in terrain height, so that large plain parts can be covered by few large triangles.
Since trimeshes and height-fields share many routines for mesh traversal, please look into the trimesh chapter (11.8.9) for more information about that.

Fig. 11.8 HeightField representing uneven surface.
Like trimeshes used as terrains, height-fields make use of a bottom margin in order to have a safeguard in case objects tunnel downwards in local z-direction through the triangle surface.
11.8.13.1. HeightField creation
The height values in a height field can either be specified through a call to agxCollide::HeightField::setHeights() which accepts a vector in row matrix order or via a agxUtil::HeightFieldGenerator(), which can read data from an image (.png) or a raw binary file (no endian handling supported).
HeightField(size_t resolutionX, size_t resolutionY, agx::Real sizeX, agx::Real sizeY, agx::Real bottomMargin=agx::Real(1));
11.8.13.2. Modifying parts of a HeightField
The height values in a height field can also be changed in only a part of the whole shape. One possibility is by calling a version of agxCollide::HeightField::setHeights() which specifies which rectangular part of the grid to modify.
bool setHeights(const agx::RealVector& heights,
size_t minVertexX, size_t maxVertexX, size_t minVertexY, size_t maxVertexY);
Another possibility is to set heights at specific points in the grid using the function agxCollide::HeightField::setHeight().
void setHeight(size_t xIndex, size_t yIndex, agx::Real height);
Note
All triangles around a changed height have to be updated.
This update includes a recalculation of the triangle normal, as well as an update of the bounding volume hierarchy.
Changing a single height will involve 6 updated triangles.
Changing several heights within a rectangle can be done faster by using agxCollide::HeightField::setHeights() rather than agxCollide::HeightField::setHeight(), since this makes it unnecessary to update triangles several times.
11.8.13.3. HeightFields for dynamic simulation
There can be cases where it is of interest to combine the ease of modification of a height field with dynamical simulation, by making the height field part of the collision detection representation of an agx::RigidBody which is simulated dynamically.
Since height-fields are generally assumed to be part of the static scenery, their mass properties are not calculated in the general case, since this comes with some computational cost.
In order to get the mass-properties updated for dynamic simulation, call the method agxCollide::HeightField::setDynamic().
In order to compute these, a sort of box-shape is assumed for the height-field, where the top has a relief defined by the heights, the sides go downwards at the borders of the grid, and the bottom is a rectangle parallel to the z plane at a position given by a specified minimum height. To specify this height, use agxCollide::HeightField::setMinAllowedHeight().
Note
When changing parts of the height-field, the mass properties will not be updated.
Instead, once all the updates are done and the new mass properties are needed for dynamic simulation, one should call agxCollide::HeightField::calculateMassProperties() which will recalculate the mass properties for the whole height-field and can potentially be costly. This might be optimized in a future release.
11.8.14. Mesh reader
The class agxIO::MeshReader is capable of reading a number of 3D Mesh formats into mesh data that can be used to create a Trimesh or Convex shapes for collision detection.
The enum agxIO::MeshReader::FileExtension lists all available formats. Most of the readers (with an exception to .shl) are utilizing the (Open Asset Importer Library) library for parsing the mesh files.
Note
Currently the MeshReader will concatenate all meshes into one mesh.
File extension |
Description |
|---|---|
obj |
Wavefront Obj |
shl |
Shell data format |
fbx |
Filmbox AutoDesk |
assimp |
AssImp reader/writer |
dae |
Collada |
blend |
Blender 3D |
3ds |
3ds Max 3DS |
ase |
3ds Max ASE |
gltfb |
Binary GL Transmission format |
gltf |
Ascii GL Transmission format |
xgl |
XGL |
zgl |
ZGL |
ply |
Stanford Polygon Library |
dxf |
AutoCAD DXF |
lwo |
LightWave |
lws |
LightWave Scene |
lxo |
Modo |
stl |
Stereolithography |
x |
DirectX X |
ac |
AC3D |
ms3d |
Milkshape 3D |
scn |
TrueSpace |
xml |
Ogre XML |
irrmesh |
Irrlicht Mesh |
irr |
Irrlicht Scene |
mdl |
Quake I |
md2 |
Quake II |
md3 |
Quake III Mesh |
pk3 |
Quake III Map/BSP |
md5 |
Doom 3 |
smd |
Valve Model |
m3 |
Starcraft II M3 |
unreal3d |
Unreal |
q3d |
Quick3D |
off |
Object File Format |
ter |
Terragen Terrain |
ifc |
Industry Foundation Classes (IFC/Step) |
ogex |
Open Game Engine Exchange(.ogex) |
11.8.15. Composite Shapes
Composite geometries are geometries containing more than one Shape. This can be useful when building more complex geometries from primitives.
There are basically two ways of creating a more complex Geometry structure around a rigid body.
Create a geometry g1, add shapes with relative transformations that builds up the final geometry. This also means that g1 can have only one material. (Material is bound per Geometry). Then, create a body b1 and add the created composite geometry g1.
Create a body b1, create the geometries needed g1, g2, … and for each geometry add shapes (Box, Sphere, …). Then, add each geometry to the body. In this case each geometry g1, g2… can each have different materials.
Note
There are two limitations when using composite shapes:
If the single shapes forming the composite shape do not overlap, interacting objects might get in between them exactly where they touch. This might happen since the single shapes which the composite shape consists of do not know about each other. Therefore it is recommendable to let shapes overlap.
However, when having overlapping shapes, the automatic mass property computation will count the overlapping volume twice. So here, manual mass property computation has to be used.
11.9. Shape colliders
A shape collider is a class that is responsible for calculating contact data between two shapes. The table below shows the available shapes and for which pair of shapes the AGX collision engine currently can calculate contact data.
11.9.1. Collider Matrix
In the following table, an overview over the functionality of colliders for different shape combinations is given. Reduced functionality means that basic functionality is given, but might have to be improved in the future in order to work perfectly in all purposes. Plane and HeightField make only sense as static geometries and can therefore not collide with themselves/each other.
Box |
Capsule |
Convex |
Cylinder |
Line |
Plane |
Sphere |
Trimesh |
Composite |
HeightField |
Cone |
HollowCone |
HollowCylinder |
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Box |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
(×) |
(×) |
(×) |
Capsule |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
(×) |
(×) |
(×) |
Convex |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
(×) |
(×) |
(×) |
Cylinder |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
Line |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
(×) |
(×) |
Plane |
X |
X |
X |
X |
X |
— |
X |
X |
X |
— |
|||
Sphere |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
(×) |
(×) |
(×) |
Trimesh |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|||
Composite |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
(×) |
(×) |
(×) |
HeightField |
X |
X |
X |
X |
X |
— |
X |
X |
X |
— |
|||
Cone |
(×) |
(×) |
(×) |
X |
X |
(×) |
(×) |
X |
X |
X |
|||
HollowCone |
(×) |
(×) |
(×) |
X |
(×) |
(×) |
(×) |
X |
X |
X |
|||
HollowCylinder |
[×] |
[×] |
(×) |
X |
(×) |
[×] |
[×] |
[×] |
(×) |
[×] |
X |
X |
X |
11.9.2. Point, normal and depth calculation
In case of an intersection between two shapes, a shape collider will report one or more contact points. Each contact point consists of
A point p,
a normal n,
a depth d.
The normal n points in the direction which lets shape1 move out of shape2.
The depth d measures how much shape 1 would have to be moved out of shape2 along normal n in order to resolve the overlap and thus have the two shapes just touching.
The point p is placed halfway between the two points corresponding to the surfaces of the two shapes, so that \(p_{shape_1 } = p- n * d * 0.5\) and \(p_{shape_2 } = p+ n * d * 0.5\).
11.9.3. Results for contacts with Line Shapes
The Line Shape is special in that its use is not in rigid body simulation, but in other fields as e.g. mouse picking or depth computation for unknown geometries. Therefore, the computation of contact point, normal and depth differs from that of the other Shapes.
The Line Shape represents mathematically a line segment, defined by two points \(P_0\) and \(P_1\), which define the non-normalized Line direction \(d = P_1- P_0\).
The Line can thus be presented as: \(P_0+ t \ d,0 \le t \le 1\).
If a Line intersects a Shape, the first point in contact \(P_c\) along the infinite version of the line is reported as contact point. The Shape surface normal is reported as contact normal. The parameter \(t_c\) is the value which realizes \(P_c= P_0+ t_c d\).
The depth is \((1 - t_c )*|P_0-P_1 |;\) this corresponds to how long the Line has to be pushed back in its direction in order to just touch the overlap point \(P_c\).
Exceptions:
For mesh-based shapes (Trimesh, HeightField and at the moment also Convex), lines which are completely inside the shape will not create any contact.
The line-line collider will create one contact point with a normal which is orthogonal to both lines and a depth of 0.
11.10. Storing renderable data in shapes: agxCollide::RenderData
agxCollide::RenderData is a class which can be used for storing renderable data together with a shape.
// Create a RenderData object
agxCollide::RenderDataRef renderData = new agxCollide::RenderData;
// Specify the vertices
agx::Vec3Vector vertices;
renderData->setVertexArray( vertices );
// Specify the normals
agx::Vec3Vector normals;
renderData->setNormalArray( normals );
// Specify the indices, which constructs Triangles
agx::UInt32Vector indices;
renderData->setIndexArray( indices, agxCollide::RenderData::TRIANGLES);
// Store a diffuse color
renderData->setDiffuseColor( agx::Vec4(1,0,1,1) );
This data can then be associated with an agxCollide::Shape:
gxCollide::ShapeRef shape = new agxCollide::Sphere(1.0);
shape->setRenderData( renderData );
During serialization to disk, this data will also be stored together with a shape. Later it can be retrieved with the call:
agxCollide::RenderData *renderData = shape->getRenderData();
In the sample coupling to OpenSceneGraph, agxOSG namespace, the function agxOSG::createVisual( geometry, agxOSG::Group *) will parse this render data and create a visual representation based on the RenderData (if available), otherwise it will use the specified shape when the renderable data is created.
11.11. Mass Properties
agx::MassProperty is a class which stores and handles the mass properties of a rigid body namely the heavy and effective mass of a rigid body.
Whenever Geometries are added/removed to/from a rigid body with the methods
RigidBody::add(Geometry*)
RigidBody::remove(Geometry*),
the inertia tensor is recalculated by default, unless a previous call to RigidBody::getMassProperties()::setAutoGenerate(false) has been done.
In this case the inertia tensor and masses will NOT be updated when geometries are added and removed.
Attention
Currently, automatic mass property calculation (incremental or not) assumes all geometries and shapes to be disjoint (non-overlapping). If they overlap, the effect of this assumption is that the overlapping volume will be counted twice into mass and inertia computation. It is recommended to set the mass properties manually in this case.
An explicit inertia tensor can also be specified manually with the call:
body->getMassProperties()->setInertiaTensor(I);
where I can either be a SPDMatrix3x3 (semi positive definite) matrix or a Vec3 specifying the diagonal elements of the inertia tensor.
The method MassProperties::setInertiaTensor has a second parameter specifying whether the inertia tensor should be automatically recalculated, when set to false, the Inertia tensor for a rigid body will not be updated to reflect changes in associated Geometries.
During the calculation of mass properties, the density from the specified materials (described later) will be used to calculate the final mass.
If no mass is specified explicitly for the body, the calculated mass will be used.
If on the other hand the mass have been set by the user with the method RigidBody::getMassProperties()::setMass(), this mass will be used for the final result.
Unless the setAutoGenerate method has been called for a rigid body, the center of mass and inertia tensor will be updated for most operations such as adding/removing geometries, removing shapes from geometries. However there are a number of operations that will NOT be detected, and hence the user has to tell the body to update its mass properties:
Transforming geometries relative the body after they are added to the body.
Changing material properties (density) for any geometry added to a body.
Transforming shapes that is part of a geometry associated to a body.
In the above cases the mass properties can be updated with a call to:
agx::RigidBody::updateMassProperties(agx::MassProperties::AUTO_GENERATE_ALL);
If you only want to update the inertia tensor you can change the argument to updateMassProperties. For more information see the SDK documentation.
11.12. Adding user forces
The class agx::RigidBody has the following methods for adding forces and torques:
addForce(), addForceAtPosition(), addForceAtLocalPosition(), addTorque().
These added forces are cleared after a time step has been taken in the simulation.
The force added to a rigid body during the last timestep (including the forces introduced by the user via addForce/addForceAtPosition/addTorque , or via force fields etc. – however, NOT the ones from contacts and constraints!) can be accessed with the methods: RigidBody::getLastForce() and RigidBody::getLastTorque()
11.13. ForceFields
The class agx::ForceField can be used to induce user forces on all or a selected part of the bodies in a DynamicsSystem. It is derived from agx::Interaction.
#include <agx/ForceField.h>
class MyForceField : public agx::ForceField
{
public:
MyForceField() {}
~MyForceField() {}
// Implement this method to add forces/torques of all or selected bodies
void updateForce( DynamicsSystem *system );
};
// Create the force field and add to the DynamicsSystem.
agx::InteractionRef forceField = new MyForceField;
simulation->getDynamicsSystem()->add( forceField );
For a more thorough example, see tutorial_bodies.cpp in <agx>/tutorials/agxOSG/tutorial_bodies.cpp
11.14. GravityField
Gravitational forces should be applied through an instance of an agx::GravityField.
The reason for this is that certain mechanics inside for example the wire implementation (agxWire::Wire) needs to know the individual gravity for each body.
By default, an instance of a class agx::UniformGravityField is created in DynamicsSystem, with the default acceleration of G = 9.80665 m/s2.
Another gravitational model is agx::PointGravityField, which will add a force towards a specified origin point.
This model can be used for simulating the gravity on the surface of the earth.
To register a gravity field with the simulation the following call is done:
agxSDK::SimulationRef sim = new agxSDK::Simulation;
sim->setGravityField( new agx::PointGravityField );
Simulation::setUniformGravity and Simulation::getUniformGravity are just wrapper methods to simplify the use of the standard uniform gravity.
A call to Simulation::setUniformGravity() will return false if the current gravity field model is not a agx::UniformGravityField.
11.14.1. CustomGravityField
The standard gravity fields (UniformGravityField and PointGravityField) are implemented as computational kernels to achieve best possible performance. For certain situations, for example when simulating micro-gravity on a asteroid, a custom gravity field might be required.
To implement a custom gravity field, a class that derived from agx::CustomGravityField is created. The actual code for calculating the gravity is implemented in the virtual method calculateGravity.
The overhead compared to the standard gravity fields is the call to virtual method which should be small.
It is however important to remember that the method calculateGravity() will be called simultaneously from several threads if AGX is using more than one thread. This means that the method must be made thread safe.
class MyGravityField : public agx::CustomGravityField
{
public:
MyGravityField() {}
/// overidden method to calculate the gravity for a point in 3D Space
virtual agx::Vec3 calculateGravity(const agx::Vec3& position) const
{
return position*-1;
}
protected:
~MyGravityField() {}
};
// Register the gravity field with the simulation
simulation->setGravityField( new MyGravityField() );
11.15. Material
The material of a geometry will define how the geometry will get affected and affect the rest of the system. A material contains definitions of friction, restitution, density and other parameters that describe the physical surface, bulk and line attributes of a material. A material can be associated to a geometry with the method:
agxCollide::Geometry::setMaterial(agx::Material*)
An important thing to remember is that the name of a material has to be unique. Adding two materials with the same name will result in that only the first will be used in the system.
New materials must be registered with the agxSDK::MaterialManager before they can be used in the simulation (which is done when the material is added to the simulation).
When two geometries collide, the resulting contact parameters from the two involved materials are derived into an agx::ContactMaterial.
The default contact material function can be overridden by adding explicit contact materials to the material manager.
Materials consist of three sub-classes which can be accessed through the calls:
material->getSurfaceMaterial();
material->getBulkMaterial();
material->geWireMaterial();
To complement the Material API, AGX also contains a Material Library with some predefined material properties that can be loaded and used as a starting point when designing simulations. See further in the Material Library section.
11.15.1. SurfaceMaterial
This class defines the behavior/surface attributes for contacts between geometries using two materials. The attributes currently available are:
Roughness – Corresponds to friction coefficient, the higher value, the higher friction.
Adhesion – determines a force used for keeping colliding objects together.
Viscosity – Defines the compliance for friction constraints. It defines how “wet” a surface is.
ContactReduction - Specifies whether contact reduction should be enabled for this material.
11.15.1.1. Roughness
The roughness describe what potential friction this material would have when it interacts with another material. The exact friction coefficient is calculated for the implicit contact material using the following equation: \(friction=\sqrt(roughness_1 \times roughness_2)\)
11.15.1.2. Adhesion
Adhesion defines an attractive force that can simulate stickiness. It operates only on bodies that have colliding geometries, i.e. it is not a general force field.
Adhesion is set using two parameters:
SurfaceMaterial::setAdhesion( adhesionForce, adhesiveOverlap );
adhesionForce specifies a force >=0, that is an upper bound of the attractive force acting between two colliding rigid bodies in the normal direction.
adhesiveOverlap is an absolute distance that defines the contact overlap where the adhesive force is active. Because that the adhesive force only acts upon overlapping rigid bodies, it is important to specify an overlap > 0. Otherwise a separating force would immediately (within a timestep) cause two bodies to separate, hence no adhesive force would then act on the bodies. The adhesiveOverlap is a safe zone to ensure that there will be time for the adhesiveForce to act.
Because the adhesive force operates only in the normal direction of the contact, it is also important to increase the roughness/friction to get a sticky behavior also in the friction direction.
\(max\_adhesive\_force \approx adhesiveOverlap / contact\_compliance\)
The adhesion distance will change the depth of the resting contact as seen in Fig. 11.9:.
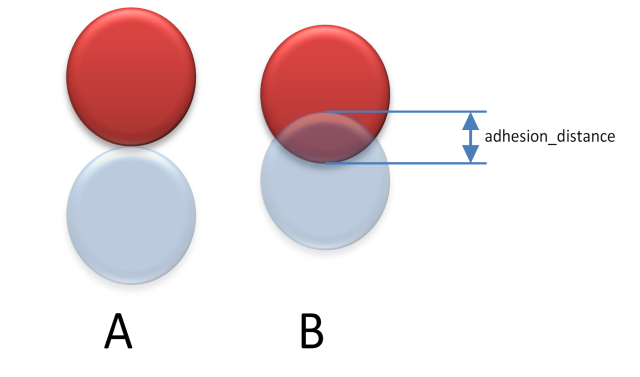
Fig. 11.9 A: no adhesion. B: adhesion_distance=r/2
The resulting adhesion parameters of an implicit contact material is calculated as \((adhesion_1+adhesion_2, min(adhesiveOverlap_1,adhesiveOverlap_2)\)
11.15.1.3. Surface viscosity
The viscosity of a surface material is the same thing as compliance but for friction in contacts. The resulting viscosity of an implicit contact material is calculated as \(viscosity = viscosity_1 + viscosity_2\)
11.15.1.4. Contact Reduction
This parameter specifies whether contact reduction should be enabled for this material. If two geometries overlap, the resulting contact material will get contact reduction enabled only if both materials have contact reduction enabled (logical and).
11.15.2. BulkMaterial
This class defines the density and other internal attributes of a simulated object. Lines use for example YoungsModulus and PoissonsRatio to calculate bending stiffness etc.
Attributes are:
Density
YoungsModulus – Stiffness of the material. Used when calculating contacts and the bending behavior of lines.
Viscosity – Used for calculating restitution.
Damping – Used for controlling how much time it should take to restore the collision penetration. A larger value will result in “softer” contacts.
11.15.2.1. Density
The density is used for calculating the mass of the rigid body from the volume of the geometry.
11.15.2.2. YoungsModulus
This specifies the stiffness of the contact between two interacting geometries/bodies. The resulting stiffness/young’s modulus for an implicit contact material is calculated as \((Y_1 \times Y_2) \div (Y_1 + Y_2)\)
11.15.2.3. Bulk viscosity
This defines the “bounciness” of an object or restitution in the contact material. The resulting restitution of an implicit contact material is calculated as \(restitution=\sqrt((1-viscosity_1)\times(1-viscosity_2))\)
11.15.2.4. Damping Time
This defines the time it should take for the solver to restore an overlap. A higher value will lead to smaller restoration forces since the overlap should be restored slower. The resulting damping time of an implicit contact material is calculated as \(damping = max(damping_1, damping_2)\)
11.15.3. WireMaterial
Defines the behavior when a geometry with this material collides with a wire. Determines the stick and slide friction. When a wire is colliding with a geometry (where the wire is overlapping an edge of a box/trimesh, or onto a cylinder), a ShapeContactNode is created. This node is allowed to slide along the edge and also in the direction along the wire. To solve for the normal force, a 1D solver will analyze the system and solve how the contact node is allowed to move, depending on masses, gravity, physical properties in the wire and the tension in the wire.
Damping and Young’s Modulus can be specified for two attributes in the wire material:
Bend – Constraint which tries to straighten a wire.
Stretch - Constraint which works against stretching the wire.
For more information, see the SDK documentation on Material.
11.15.4. ContactMaterial
The class agx::ContactMaterial is used by the system to derive the actual material attributes when two materials collide.
It can also be used to explicitly define a material used at contact calculations.
All attributes found in the surface, bulk and line material is represented in the ContactMaterial, which is later used by the solver.
AGX use by default a contact point based method for calculating the corresponding response between two overlapping geometries.
There is also a different method available which is named area contact approach. This method will try to calculate the spanning area between the overlapping contact point. This can result in a better approximation of the actual overlapping volume and the stiffness in the response (contact constraint).
In general, this will lead to slightly less stiff, more realistic contacts and therefore the Young’s modulus value usually has to be increased to get a similar simulation results as running the simulation without the contact area approach.
// Create a contact material based on two agx::Material’s m1 and m2
agx::ContactMaterial *cm = simulation->getOrCreateContactMaterial(m1, m2);
// When two geometries collide, where m1 and m2 is involved, the contact area approach
// will be used.
cm->setUseContactAreaApproach( true );
agx::Real minElasticRestLength=0.0005, agx::Real maxElasticRestLength=0.05;
cm->setMinMaxElasticRestLength(minElasticRestLength, maxElasticRestLength);
The above code line determines the contact depth-span in which the material is elastic. AGX calculates this distance, but the material settings will put limits on this value. It can not be less than the minimum material rest length or greater than the maximum material rest length. For this reason, the minimum material rest length can not be greater than the maximum material rest length. For the theory background, see Contact mechanics (Elastic Foundation Model).
11.15.5. Overriding ContactMaterial friction and restitution
A GeometryContact contains collision information between two geometries. One ContactMaterial is assigned to each GeometryContact. Hence all contact points in the GeometryContact would use the same friction and restitution.
To support different values per contact point, the ContactMaterial values for friction and restitution are used to initialize the corresponding values for each ContactPoint in the GeometryContact.
These values can then be modified as needed on a per-point basis in a user callback, for example via a ContactEventListener or via the preCallback in a StepEventListener. These events are after Space have performed collision detection, but before the solver used these values.
11.16. Calculating contact friction
At present, there is no difference between static and kinetic friction coefficients. According to published data and common models, these two coefficients differ by 10-20%. This is relevant in simulation of gear dynamics but not in most other cases. Friction coefficients do depend on the two materials in contacts.
So given material1 with roughness 0.5 and material2 with roughness 0.2, what friction coefficient should be used when these two materials get in contact? There is no clear picture of how to calculate this resulting friction coefficient in the general case. Therefore, by default, the resulting friction when material1 and material2 collides will be the geometric averaged value:
sqrt(material1.roughness*material2.roughness) = 0.31623
This is of course a crude approximation which does not have any relation to the real world physics. To overcome this, AGX supports explicit ContactMaterial, see Section 11.16.2.
Contacts are handled in two separate stages, namely, impact, and resting contact. Impacts correspond to a rigid body which is found in geometric interference at the beginning of a step with sufficiently large incident velocity, i.e., when the relative velocity projected on the separating normal is sufficiently negative. During impact resolution, the impacting energy is approximately restituted to the level of the restitution coefficient. This is done by computing an impulsive stage which preserves all constraints but applies a Newton restitution model on impacting contacts, with post impact velocity a fraction of the pre-impact incident velocity. That fraction is the restitution coefficient and it is usually a number between 0 and 1. The restitution coefficient applies to all pairs of rigid bodies and is part of the pair-wise contact properties. Because we do not locate the exact time of impact, there can be a small decrease in energy even if restitution is exactly 1.
After impact, constraint regularization and stabilization come into play. From the modeling perspective, this is no more and no less than a spring/damper system. Numerically, the spring and damper system is unconditionally for nonzero damping.
The two parameters are accessible as contact compliance (1/YoungsModulus) and damping coefficient in the material properties.
Compliance is just the inverse of the desired spring constant, with the usual units.
The AGX damping parameter (also called “Spook damping parameter”) has units of time for technical reasons.
Use the functions in agxUtil::Convert in order to convert from viscous damping coefficient to AGX’ damping coefficient.
There are basically two ways of setting up the material table for a complete system: defining implicit or explicit material properties.
11.16.1. Defining implicit Material properties
By creating an agx::Material, setting the properties, assigning it to a geometry and adding it to the Simulation, we have told the system that this geometry is created from some kind of material.
When this geometry collides with another geometry, the pair of materials are used to calculate the resulting agx::ContactMaterial.
This is a fairly easy way of creating the materials in the system, as every pair of materials does not really have to be known in beforehand.
The calculation of material properties for the implicit contact material cm between material m1 and m2 is done as follows:
cm.surfaceFrictionCoefficient = sqrt(m1.roughness*m2.roughness)
cm.restitution = sqrt((1-m1.viscosity) * (1-m2.viscosity))
cm.adhesion = m1.adhesion+m2.adhesion
cm.youngsModulus = m1.youngsModulus * m2.youngsModulus / ( m1.youngsModulus + m2.youngsModulus )
cm.damping = max(m1.damping, m2.damping)
cm.surfaceViscosity = m1.surfaceViscosity+m2.surfaceViscosity
The frictional parameters for wire friction are using the same geometric medium as surface friction.
Note
We recommend that explicit contact material are used. This will give a better control over the simulation result instead of relying on the automatically calculated values in an implicit contact material.
11.16.2. Defining explicit ContactMaterial properties
If the actual values used in the friction solver has to be known exactly, the above method is not appropriate. Instead an explicit material table should be created.
This can be done by associating two agx::Material, M1 and M2 to one user created agx::ContactMaterial CM.
So whenever the two materials M1 and M2 are involved in a contact, the attributes of CM are used. However, the following attributes of M1 and M2 still have to be set, to correctly calculate the mass properties of a RigidBody and to have correct behavior for LineConstraints.
BulkMaterial::setDensity()
BulkMaterial::setYoungsModulus()
At contact between two instances of agx::Material the following list of attributes are used and should therefore be set to the required value:
ContactMaterial::setRestitution()
ContactMaterial::setFrictionCoefficient()
ContactMaterial::setDamping()
ContactMaterial::setEnableContactReduction()
FRICTION |
PLASTIC |
METAL |
WOOD |
|---|---|---|---|
Plastic |
?? |
0.7 |
0.3 |
Metal |
— |
?? |
0.2 |
Wood |
— |
— |
?? |
Table showing friction coefficients between different materials, defined via explicit or implicit contact materials.
To build a table of explicit materials each ContactMaterial are associated to two instances of agx::Material. Code for setting up this table could look like:
agx::MaterialRef wood = new agx::Material("Wood");
agx::MaterialRef plastic = new agx::Material("Plastic");
agx::MaterialRef metal = new agx::Material("Metal");
// Define the material for plastic/metal
agx::ContactMaterialRef plastic_metal = new agx::ContactMaterial(plastic, metal);
plastic_metal->setRestitution( 0.6 );
plastic_metal->setFrictionCoefficient( 0.7 );
plastic_metal->setYoungsModulus( 0.1E9 ); // GPa
// Define the material for wood/metal
agx::ContactMaterialRef wood_metal = new agx::ContactMaterial(wood, metal);
wood_metal->setRestitution( 0.2 );
wood_metal->setFrictionCoefficient( 0.2 );
// Define the material for wood/plastic
agx::ContactMaterialRef wood_plastic = new agx::ContactMaterial(wood, plastic);
wood_plastic->setRestitution( 0.4 );
wood_plastic->setFrictionCoefficient( 0.3 );
wood_plastic->setYoungsModulus( 3.654E9 ); // GPa
// Add ALL materials to the simulation
simulation->add(wood)
simulation->add(metal)
simulation->add(plastic)
simulation->add(plastic_metal);
simulation->add(wood_metal);
simulation->add(wood_plastic);
The above code example still leaves to the system to automatically derive the ContactMaterial for wood/wood, plastic/plastic and metal/metal.
11.16.2.1. ContactReduction
This parameter controls whether contact reduction should operate on the contacts where this contact material is used. For details, see Section 38.7.
11.16.2.2. Contact Area approach
If set to “true”, an approximation to the contact area will be geometrically computed for each contact involving this contact material. For each contact, its area will then be evenly distributed between its contact points. The contact compliance will be scaled with the inverse of the area for each contact point.
Note
This is an experimental feature, which has been tested on contacts involving meshes and boxes, but with a cruder approximation for contacts involving spheres or capsules. Recommended for contact mechanics with a higher level of fidelity, such as grasping (involving meshes/boxes). If set to “false”, the unity area will be assumed (default).
// Define the material for wood/plastic
agx::ContactMaterialRef wood_plastic = new agx::ContactMaterial(wood, plastic);
wood_plastic->setUseContactAreaApproach(true);
11.16.3. Friction model
There are several friction model implementations in AGX Dynamics, each with different characteristics. They are commonly defined around the primary (\(\hat u\)) and secondary (\(\hat v\)) friction directions. \(\hat u\) is orthogonal to \(\hat v\) and both are orthogonal to the contact normal \(\hat n\). The plane spanned by \(\hat u\) and \(\hat v\) is called the friction plane and the friction forces are applied in this plane at the contact point \(\bar p\).
Finding an accurate friction force is nonlinear, i.e., the friction force depends on the normal force and the normal force depends on the friction force. This nonlinearity affects how quick a solver will find a solution, and how accurate the results are. The different friction models and choice of solve type enables the configuration possibility to have simulations with (relatively) computationally expensive, precise, to computationally inexpensive, acceptable, results.
In AGX Dynamics, a nonlinear frictional contact is solved for the three force directions along \(\hat u\), \(\hat v\) and \(\hat n\) such that,
where \(F_n\) is the normal force, \(F_u\) and \(F_v\) the primary and secondary friction forces and \(F_f\) the resulting friction force. This formulation is consistent with the ideal Coulomb friction law; \(F_f \leq \mu |F_n|\), when \(\hat u\), \(\hat v\), \(\mu_u^\prime\) and \(\mu_v^\prime\) are appropriately selected. AGX Dynamics different friction models and solvers supports this computation and various approximations that are more easily solved.
Even though the values of \(\mu_u^\prime\) and \(\mu_v^\prime\) depends on the implementation of the friction model, consider them as friction coefficients constrained by the given primary and secondary friction coefficients \(\mu_u\) and \(\mu_v\) such that,
where \(\mu_u\) and \(\mu_v\) can be assigned to explicit contact materials:
agx::ContactMaterialRef cm1 = new agx::ContactMaterial(m1, m2);
// Both primary and secondary friction coefficients are assigned
// the given value - isotropic friction.
cm1->setFrictionCoefficient(0.4);
// Anisotropic friction, where primary != secondary friction coefficient.
agx::ContactMaterialRef cm2 = new agx::ContactMaterial(m1, m3)
cm2->setFrictionCoefficient(0.4, agx::ContactMaterial::PRIMARY_DIRECTION)
cm2->setFrictionCoefficient(0.2, agx::ContactMaterial::SECONDARY_DIRECTION)
Note
The primary and secondary friction directions, \(\hat u\) and \(\hat v\), are by default aligned with worlds’ principal axes. See Oriented friction models or Custom friction models for more information and examples how to configure the friction directions.
The ideal Coulomb friction law states that, given a friction coefficient \(\mu\), the resulting friction force is \(|F_f| \leq \mu |F_n|\). This means that, given a known (solved for) normal force \(F_n\), \(F_f\) will be constrained within a circle in the friction plane (segmented circle below). However, it’s common in numerical physics (including some friction model implementations in AGX Dynamics) to approximate \(\mu_u^\prime = \mu_u\) and \(\mu_v^\prime = \mu_v\), which won’t result in \(F_f\) to be within the circle, but rather within a “box”/rectangle in the friction plane (solid line below). That’s why friction model names may include the name “box”, such as BoxFrictionModel and ScaleBoxFrictionModel, while IterativeProjectedConeFriction can find an accurate \(F_f\) within the circle.
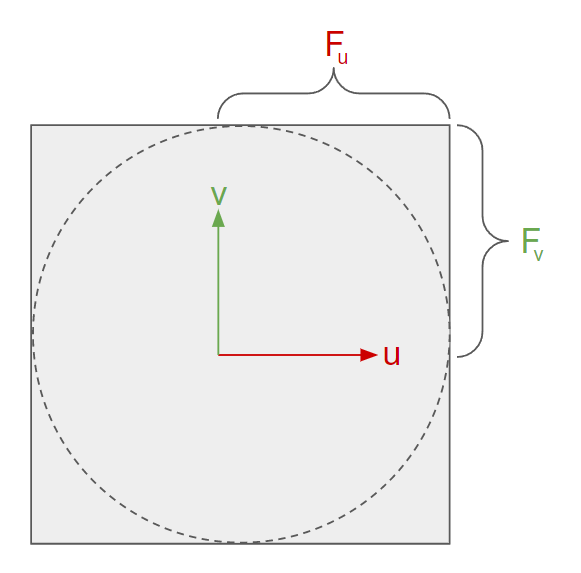
Fig. 11.10 Friction forces \(F_u\), \(F_v\) and resulting friction force \(F_f\) is desired (for accuracy) to be within the segmented circle in the friction plane. “Box” friction models are an approximation resulting in the desired (ideal) circle to be a rectangle (solid) in the friction plane.
Worse case scenario for box friction models is when the resulting friction force \(F_f\) is at \(45^{\circ}\) (and \(45^\circ + 90^\circ = 135^\circ\) etc.) in the friction plane. I.e., when \(F_u = \mu_u F_n\) and \(F_v = \mu_v F_n\), then
so \(F_f\) is overestimated by a factor of \(\sqrt{2} \approx 1.41\) in the worse case directions. The symptoms of the built in anisotropy of the box algorithm can be mitigated in some scenarios by using Oriented friction models or eliminated using IterativeProjectedConeFriction. There are also relevant example implementations in Custom friction models.
More general than box or circle (defined for a given normal force \(F_n\)), an ideal friction model is required to have
a resulting friction force \(F_f\) within the so called friction cone (A in the picture below), for any given normal
force. Box friction approximation models will not recover the desired friction cone where the resulting friction
forces \(F_f\) are instead within an inverted friction pyramid (B in the picture below). Note that box friction
models are optimal for convergence and performance of a solver, especially when the solver is using direct solving methods, e.g.,
agx::FrictionModel::DIRECT Solve type in AGX Dynamics.
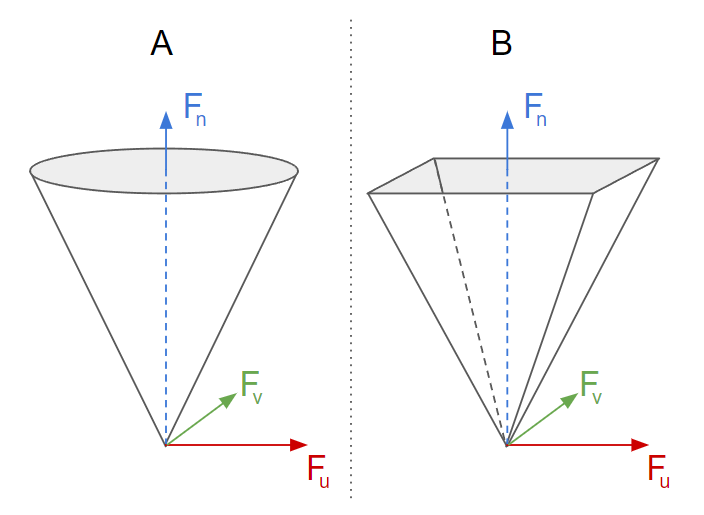
Fig. 11.11 The resulting friction forces should, ideally, be on the surface or inside the friction cone (A). It’s convenient and (computationally) efficient to approximate \(\mu_u^\prime = \mu_u\) and \(\mu_v^\prime = \mu_v\) which will result in the final friction force to be on the surface of or inside of the (inverted) friction pyramid (B).
In the different friction model implementations below, assume that the following code has been executed:
using namespace agx;
// Create two materials
MaterialRef wood = new Material("wood");
MaterialRef steel = new Material("steel");
// Create two geometries with material wood and steel.
agxCollide::GeometryRef geom1 = new agxCollide::Geometry();
geom1->setMaterial(wood);
agxCollide::GeometryRef geom2 = new agxCollide::Geometry();
geom2->setMaterial(steel);
// Create a contact material that will be used when steel collides with wood
ContactMaterialRef steelWood = simulation->getMaterialManager()->getOrCreateContactMaterial(wood,
steel);
11.16.3.1. BoxFrictionModel
This friction model has fixed friction bounds throughout the solve stage. It’s (CPU) performance vice “optimal”, but is in general not a suitable friction model in simulations where friction and/or accuracy is important.
Normally one would expect the friction force to be: \(|F_f| \leq \mu |F_n|\), but since the normal force magnitude \(|F_n|\) is unknown before the solver starts, the size of the normal force has to be guessed/approximated. When guessed, the masses of dynamic rigid bodies involved are used so that the order of magnitude matches the scale of the interaction: \(|F_n| = (m_1 + m_2) g\), where \(m_1\) and \(m_2\) are masses and \(g\) the default gravity acceleration (9.80665…). In ConstantNormalForceOrientedBoxFrictionModel, the normal force magnitude is customizable.
If Contact Warmstarting is enabled, the normal force from the previous time step is used as approximation. This approximation is of course better than using the masses, but is in general also not accurate due to the slow propagation of the nonlinearity of a frictional contact.
BoxFrictionModelRef boxFriction = new BoxFrictionModel();
// Use box friction as the friction model for this contact material
steelWood->setFrictionModel(boxFriction);
11.16.3.2. ScaleBoxFrictionModel
This friction model has dynamic friction bounds throughout the solve stage, hence “scale” in the name. I.e., the friction bounds will be updated given the current normal force, such that,
and note the “box” approximation \(\mu_u^\prime = \mu_u\) and \(\mu_v^\prime = \mu_v\) (B in Fig. 11.11 above).
The nonlinear response of the friction force given the normal force is computationally more expensive but results in accurate friction, even though the forces may exceed the Coulomb friction law in some directions (see calculation in Friction model).
ScaleBoxFrictionModelRef scaleBoxFriction = new ScaleBoxFrictionModel();
// Use scaled box friction as the friction model for this contact material
steelWood->setFrictionModel(scaleBoxFriction);
11.16.3.3. IterativeProjectedConeFriction
This friction model, with solve type SPLIT, is the default in AGX Dynamics. I.e., ContactMaterial friction
model instance is by default nullptr and this is implicitly equivalent to new IterativeProjectedConeFriction(FrictionModel::SPLIT).
The name “Iterative Projected Cone Friction” originates from an early algorithm where the friction equations were solved with an iterative solver, i.e., solve type SPLIT. For solve type DIRECT, this friction model was identical to ScaleBoxFrictionModel in AGX Dynamics 2.34.0.3 and earlier. Versions 2.35.0.0 and later includes improved direct projection algorithms finding \(\mu_u^\prime\) and \(\mu_v^\prime\) fulfilling ideal Coulomb friction (A in Fig. 11.11 above) for solve types DIRECT, SPLIT and ITERATIVE, i.e.,
where
See Fig. 11.12 below how the resulting \(\mu_{u|v}^\prime\) relates to the given (input) friction coefficients \(\mu_{u|v}\).
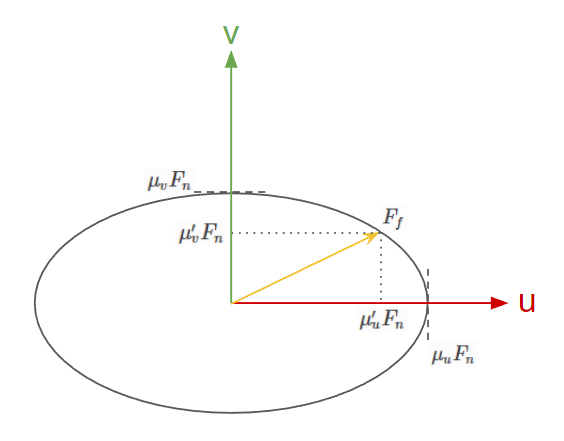
Fig. 11.12 With anisotropic friction (\(\mu_u \neq \mu_v\)), the circle in Fig. 11.10 is an ellipse, and it’s desired the resulting friction force \(F_f\) to be on the surface or within this ellipse. The solver (friction model) is responsible of finding \(\mu_{u|v}^\prime\) so that the Coulomb friction law, \(|F_f| \leq \sqrt{(\mu_u^\prime)^2 + (\mu_v^\prime)^2} |F_n|\), is fulfilled.
For solve type DIRECT, the default behavior is to make some qualified assumptions about the direction of the resulting friction force. This may result in slight overestimated friction forces in some cases, but is much more suitable for nonlinear direct methods with better stability and convergence (close to optimal ScaleBoxFrictionModel). To enable exact projections, guaranteeing the resulting friction force within the friction cone (Fig. 11.11, Fig. 11.12), use:
/**
Enable/disable exact cone projection when solve type is DIRECT. This feature
is disabled by default when it may affect the convergence of the solver. When
enabled, the friction forces will be within the friction cone at any given
resulting direction.
\param enable - enable/disable exact cone projection when solve type is DIRECT
*/
void setEnableDirectExactConeProjection( bool enable );
IterativeProjectedConeFrictionRef ipcFriction = new IterativeProjectedConeFriction();
ipcFriction->setSolveType(FrictionModel::DIRECT);
ipcFriction->setEnableDirectExactConeProjection(true);
steelWood->setFrictionModel(ipcFriction)
IterativeProjectedConeFrictionRef ipcFriction = new IterativeProjectedConeFriction();
// Use iterative projected cone friction as the friction model for this contact material
steelWood->setFrictionModel(ipcFriction);
11.16.3.4. Oriented friction models
Oriented friction models is of the same type as the ones described above but with the friction box/ellipse oriented with a given frame of reference and a primary friction direction (in the given frame).
const auto localPrimaryDirection = agx::Vec3::X_AXIS();
auto obfm = new agx::OrientedBoxFrictionModel(rb1->getFrame(),
localPrimaryDirection);
auto osbfm = new agx::OrientedScaleBoxFrictionModel(rb2->getFrame(),
localPrimaryDirection);
auto oipcfm = new agx::OrientedIterativeProjectedConeFrictionModel(rb3->getFrame(),
localPrimaryDirection);
cm1->setFrictionModel(obfm);
cm2->setFrictionModel(osbfm);
cm3->setFrictionModel(oipcfm);
Given a contact with an oriented friction model, the friction plane is calculated given the contact normal and the given primary friction direction. The secondary friction direction is orthogonal to the primary direction.
11.16.3.5. ConstantNormalForceOrientedBoxFrictionModel
This friction model is similar to OrientedBoxFrictionModel but it has some additional features:
The normal force \(F_n\) is given, resulting in the primary friction force \(F_u\) to be bound by: \(-\mu_u F_n \leq F_u \leq \mu_u F_n\) and the secondary friction force \(F_v\) to be bound by: \(-\mu_v F_n \leq F_v \leq \mu_v F_n\) – where \(\mu_u\) is the primary friction coefficient and \(\mu_v\) the secondary friction coefficient.
Contact depth dependent maximum friction forces (disabled by default), by scaling the given normal force with the depth of each contact. Enabling this feature may impact the performance but the resulting behavior of the contacting objects may be better.
11.16.3.6. Custom friction models
Custom friction models are user defined implementations of friction in AGX Dynamics. While it’s possible to recreate any native friction model implementation, the value of having a custom implementation is often due to something simulation/system/model dependent that is identified and possible to utilize as a friction model.
There are two methods possible to build the custom friction model around:
FrictionModel::initialize, assigning the initial friction bounds./** Initializes bounds given contact point (pointIndex). \param geometryContact - geometry contact \param pointIndex - point in geometry contact \param dt - time step \param ret_boundU - returned, primary direction bounds \param ret_boundV - returned, secondary direction bounds */ virtual void initialize( const Physics::GeometryContactPtr geometryContact, size_t pointIndex, agx::Real dt, agx::RangeReal& ret_boundU, agx::RangeReal& ret_boundV ) const override;
FrictionModel::calculateTangentPlane, assigning the primary (\(\hat u\)) and secondary (\(\hat v\)) friction directions./** Calculates friction plane given normal. Only valid if \p normal, \p ret_u and \p ret_v are orthogonal. \param geometry1 - first geometry in the geometry contact \param geometry2 - the other geometry in the geometry contact \param point - contact point in world coordinate system \param normal - contact normal in world coordinate system \param depth - penetration depth \param ret_u - returned, primary direction in friction plane \param ret_v - returned, secondary direction in the friction plane */ virtual void calculateTangentPlane( const agxCollide::Geometry* geometry1, const agxCollide::Geometry* geometry2, const agx::Vec3& point, const agx::Vec3& normal, const agx::Real depth, agx::Vec3& ret_u, agx::Vec3& ret_v ) const override;
The examples below are implemented in Python because there are some additional remarks compared to a C++ implementation. Converting the examples from Python to C++ is straightforward since the Python API is generated given the C++ API.
11.16.4. Solve type
The solve type of a friction model defines in which type of solver the normal and/or tangents of a frictional contact are solved. In which solver a frictional contact is solved affects performance, accuracy and stability. The default solve type is SPLIT. For more information about the different solvers in AGX Dynamics, see Direct solver, Split solver and Iterative solver, and examples in Using correct solve type.
FrictionModel* frictionModel = steelWood->getFrictionModel();
frictionModel->setSolveType(FrictionModel::DIRECT);
frictionModel->setSolveType(FrictionModel::SPLIT);
frictionModel->setSolveType(FrictionModel::ITERATIVE);
frictionModel->setSolveType(FrictionModel::DIRECT_AND_ITERATIVE);
11.16.4.1. DIRECT
The contact normals and tangents are solved with the Direct solver. Nonlinear friction models, such as ScaleBoxFrictionModel and IterativeProjectedConeFriction, will result in additional solves when the friction bounds are adjusted given the solved for normal force. The nonlinear friction models with this solve type are the most accurate but requires more calculations to find a solution.
Linear friction models, such as BoxFrictionModel, requires only a single solve when the friction bounds are fixed with an estimated normal force.
11.16.4.2. ITERATIVE
The contact normals and tangents are solved with the Iterative solver. The nonlinearity of some friction models, such as ScaleBoxFrictionModel and IterativeProjectedConeFriction, doesn’t require more calculations than the linear (approximated), which makes this solve type the most (CPU) efficient and is therefore the suitable solve type for large contact systems.
11.16.4.3. SPLIT
The contact normals are solved in both the Direct solver and the Iterative solver, while the tangents (friction) are solved with the Iterative solver with the normal forces from the direct solve as input. See Split solver for more information.
As described in the iterative solve type, solving friction with an iterative solver is more efficient than with a direct solver. This solve type will always provide the important responses of the contact normal forces and in many cases provide frictional response forces that are suitable enough in many scenarios.
The friction forces calculated in the iterative solver are transferred back to the direct solver as a weak interaction (external
force). If other interactions (e.g., constraints and/or other contacts) exists with direct solve types and are interacting with
a split contact, the direct interactions may remove some of the friction force, resulting in viscous (constant speed) slide of the
contact in the friction plane. The undesired slide can be mitigated by setting solve type DIRECT_AND_ITERATIVE on the
constraints interacting with the sliding object or, if possible, change the solve type of the friction model to DIRECT.
11.16.4.4. DIRECT_AND_ITERATIVE
Note
This solve type is experimental and may, in its default behavior, result in too large resulting friction forces.
The contact normals and tangents are solved in both the Direct solver and the Iterative solver. The contact normals and friction bounds are estimated in the Iterative solver by:
Direct solve with infinite friction bounds.
Iterative solve where the friction bounds are updated as per the Friction model this solve type is set for.
Direct solve using the resulting friction bounds from the iterative solve.
This solve type makes all friction models “linear” in the direct solver, i.e., similar to BoxFrictionModel but with the normals and friction bounds estimated with the previous direct and iterative solve in this time step.
The initial direct solve with infinite friction is a probable source to overestimated resulting friction forces. In a generic implementation
the bounds may either be zero or infinite, and with an initial direct solve without friction, the resulting friction forces are instead
underestimated. If this is a preferred solve type in your application, it may be suitable with a custom implementation
where initialize is overridden, setting the initial bounds given something application dependent, e.g.,
class MyDirectAndIterativeFrictionModel(agx.ScaleBoxFrictionModel):
@property
def initial_max_friction_force(self) -> float:
return self._initial_max_friction_force
@initial_max_friction_force.setter
def initial_max_friction_force(self, max_friction_force: float) -> None:
assert max_friction_force >= 0.0, 'Invalid initial friction force value < 0.0.'
self._initial_max_friction_force = max_friction_force
def __init__(self,
max_friction_force: float,
solve_type: int = agx.FrictionModel.DIRECT_AND_ITERATIVE):
super().__init__(solve_type)
self.__disown__()
self.initial_max_friction_force = max_friction_force
def initialize(self,
gc_ptr: agxCollide.GeometryContactPtr,
point_index: int,
dt: float,
ret_boundU: agx.RangeReal,
ret_boundV: agx.RangeReal) -> None:
# Note that it's not required to use the friction coefficient(s) here,
# the friction coefficient will be used during the following iterative
# and last direct solve.
ret_boundU.setLower(-dt * self.initial_max_friction_force)
ret_boundU.setUpper(dt * self.initial_max_friction_force)
ret_boundV.setLower(-dt * self.initial_max_friction_force)
ret_boundV.setUpper(dt * self.initial_max_friction_force)
11.17. Material Library
AGX contains some predefined material properties to help provide a starting point for the Material definitions in a simualtion. The definitions in the Material Library are generic, e.g. wood is defined, but not birch, oak or balsa tree. Those different types of wood have rather different properties, e.g. density. So for specific needs, the Materials used in a Simualtion should be defined according to your needs.
The definitions in the Material Library are limited to contain material properties and does not contain AGX implementation details. If for example a certain friction model is desired, then this has to be configured by the user.
When two materials from the material library interact, the material library is automatically searched for a predefined ContactMaterial for said Material pair. If none such ContactMaterial exists, then an implicit ContactMaterial is created and used.
The Material Library contains the following parts:
Material definitions
ContactMaterial definitiions
TerrainMaterials
BeamModelProperties
CableProperties
Note
Some classes use more than just a Material for its definitions. Examples of this is e.g.
agxCable::Cablewhich use both a Material and CableProperties,agxTerrain::Terrainwhich use Material and TerrainMaterialagxModel::BeamModelwhich use Material and BeamModelProperties
Example usage of the Material Library:
# Load into existing Material
my_material1 = agx.Material()
my_material1.loadLibraryMaterial("wood")
# Get a Material, None on failure
steel = agx.MaterialLibrary.loadMaterial("steel")
# Custom Materials can be based on items defined in the library
my_soft_steel = agx.Material(steel)
# customize my_soft_steel
# Modify the TerrainMaterial for a agxTerrain.Terrain
my_terrain.loadLibraryMaterial("dirt_1")
# Set both Material and CableProperties on a Cable:
my_cable.setMaterial(steel)
my_cable.loadLibraryProperties("cable_1")
# Some class based upon agxModel.BeamModel
my_i_beam.loadLibraryProperties("beam_1")
Classes that use properties have the method getAvailableLibraryProperties() whereas Terrain and Material have getAvailableLibraryMaterials() that can be used to inspect available items. This can also be done via agx::MaterialLibrary::getAvailableItems(item_type).
Which items that are available can also be seen by looking at the contents of <agx>/data/MaterialLibrary/<item type>/.
The different items are referenced by their short name. So for example if the Material steel is loaded, AGX searches for MaterialLibrary/Materials/steel.json. In the same way, if a CableProperty called cable_1 is requested, then the file MaterialLibrary/CableProperties/cable_1.json is search for. When a definition for a ContactMaterial is searched for, the name is the material1-material2 where the materials are in alphabetical order.
The lookup for all items in the material library is done using the RESOURCE_PATH and if you want to make AGX search at more locations, see Locating files and resources.
Note
GranularBodySystem settings in ContactMaterial
The ContactMaterial definitions all list default values used by the GranularBodySystem for GraularBody specific parameters such as rolling resistance and twisting resistance. The reason for this is to expose the values in case someone wants to define their own materials. These values are highly shape dependent and what the granulars look like have a much larger effect on the parameter values than the actual combination of materials that interact.
E.g. if the granulars that interact are spheres or boxes influence the values more than if it is wood-wood or wood-steel.
11.17.1. Adding new items to the Material Library
The material library can be extended by placing a json file in the corresponding MaterialLibrary/<item type>/ directory. Existing files can be used to see which parameters that should be defined.
When adding a Material there is one special value in the file that is important for how contact materials are found. That is the value for name. In the files provided with AGX Dynamics, the name value matches the filename, e.g. MaterialLibrary/Materials/wood.json have “name”: “wood”. It is the pair of two such names that are used when searching for a contact material when two library materials interact.
The reason for “name” is that one can have e.g. birch.json and pine.json and both use wood for name. Then interactions for the specific birch material would use the predefined contact materials that already exist for wood.
11.18. Closest point computation
Getting the closest distance between two shapes or geometries can be computed using
agxCollide::computeShapeDistance and agxCollide::computeGeometryDistance.
This feature is currently only available for convex shapes for which the method hasSupportFunction() returns true
including convex, sphere, box, convex, cylinder, capsule, cone, hollow cylinder and hollow cone.
The closest distance can be computed between two geometries computeGeometryDistance (containing one or more shapes) or between two shapes computeShapeDistance.
The transformation must always be explicitly specified, even for geometries (see below).
// Assume we have two geometries, each with a transformation.
agxCollide::GeometryRef geometry1;
agxCollide::GeometryRef geometry2;
// Closest point on each geometry
agx::Vec3 point1, point2;
// Compute the closest distance
agxCollide::ShapeDistanceResult result = agxCollide::computeGeometryDistance(
geometry1,
geometry1->getTransform(),
geometry2,
geometry2->getTransform(),
point1, point2);
// If result is success we can use the output!
if (result == agxCollide::ShapeDistanceResult::SUCCESS)
std::cerr << "Distance: " << (point2 - point1).length() << std::endl;
else if(result == agxCollide::ShapeDistanceResult::OVERLAPPING_SHAPES)
std::cerr << "Shapes are overlapping, no information available" << std::endl;
See also tutorials/tutorial_shape_distance.agxPy for more examples of how to use this functionality.
11.19. Testing user geometry against Space
In some cases it is of interest to intersect the current configuration in the collision space with some geometries, without actually inserting a new geometry into the collision space.
As soon as a geometry is inserted into space, it is a part of the simulation. Also testing for contacts in between two simulation frames can sometime be used for example for path finding etc.
There are two methods for achieving this in agxCollide::Space:
bool Space::testBoundingVolumeOverlap(
agxCollide::GeometryPtrVector& testGeometries,
agxCollide::GeometryPairVector& result,
bool skip = true );
bool Space::testGeometryOverlap(
agxCollide::GeometryPtrVector& testGeometries,
agxCollide::GeometryContactVector& result,
bool skip = true );
testBoundingVolumeOverlap will take a vector of Geometries and return pairs of Geometries with overlapping bounding volumes.
testGeometryOverlap will take a vector of Geometries and return a vector of geometry contacts, including contact points, penetration, normals etc. …
11.20. Reading forces from the simulation
Often when you build a simulation you also want to read forces/torques from the system. Assume you have built your scene with geometries, bodies, constraints and wires. Now how do you access the forces from your simulation?
Note
As in many parts of this documentation, the term “force” is here used interchangeably for a 3d force vector in contrast to a 3d torque vector and, where applicable, as a 6d vector consisting of both force and torque.
Forces can be divided into a few separate categories:
External/ForceField/Gravity forces
Constraint forces
Contact forces
11.20.1. External/ForceField/Gravity forces
Forces and torques can be applied to a body by the methods:
RigidBody::addForce, RigidBody::addTorque, etc. see 11.12.
External forces also include forces added by ForceFields, GravityFields. These external forces can at any time be read from a given rigid body with the method:
const agx::Vec3& RigidBody::getLastForce() const;
const agx::Vec3& RigidBody::getLastTorque() const;
11.20.2. Constraint forces
It is possible to read constraint forces applied to rigid bodies during the last time step for each constraint. However, it is currently not possible to ask a rigid body for its constraint forces directly - you have to keep track of the constraints attached to a specific body yourself and ask those constraints for the forces.
11.20.2.1. Constraint::getLastForce per body
For computational reasons, the calculation of constraint forces is disabled by default. To enable the computation of constraint forces call the method:
void Constraint::setEnableComputeForces(bool);
once for each constraint that you want to read forces from in the future.
Then, after the solver has been executed, you can access (e.g. with a StepEventListener in POST) the forces/torques applied to the constrained bodies with a call to:
// If you know the index of your body in the Constraint (0 or 1)
bool Constraint::getLastForce( UInt bodyIndex, Vec3& retForce, Vec3& retTorque, bool giveTorqueAtCm=false ) const;
// If you have pointer to the rigid body
bool Constraint::getLastForce( const RigidBody* rb, Vec3& retForce, Vec3& retTorque, bool giveTorqueAtCm=false ) const;
Note
Note that getLastForce is only valid when called for a rigid body with motion control DYNAMICS or KINEMATICS (not STATIC). Check the return value to detect invalid calls to getLastForce.
The returned force and torque by getLastForce are defined in the world coordinate system.
The returned torque depends on the value of the flag giveTorqueAtCm:
A value of true gives the torque in the body’s center of mass (corresponding to
RigidBody::addTorque(Vec3)),whereas the default value of false gives the value in the constraint’s attachment point r for the body, so that tau_attachment = tau_cm + r cross F
11.20.2.2. Constraint::getCurrentForce per constraint-DOF
If you are interested in obtaining the force applied by the constraint at a certain degree of freedom (in the constraint’s local coordinate system), you can use
// \return the current force magnitude (i.e., the force magnitude last time step) in given DOF >= 0 && <= NUM_DOFS
bool Constraint::getCurrentForce( UInt degreeOfFreedom) const;
Note that the degrees of freedom have different meanings for each constraint type; the enum DOF which is defined per constraint should be used.
The method getCurrentForce exists also for secondary constraints (see Section 12.15).
Attention
The naming difference in getCurrentForce and getLastForce is misleading since both methods read the forces from the same source and time. These methods will likely be renamed in the future to reflect their behavior better.
11.20.3. Contact forces
Contact forces are included in the contact data, together with contact points, normals depths, … . Contact forces are valid after the solver has been executed. You can access them (e.g. with a StepEventListener in POST) like in the following example.
Assume you want to collect the sum of the absolute values of all the contact forces (normal and friction) being applied on a specific rigid body.
One way is to explicitly iterate through all geometry contacts. This will give you the best control and will allow you to read out all the available data from contacts.
Below is an example demonstrating how to access the contact points via the agxCollide::Space object.
More examples can be found in the tutorial file tutorials/agxOSG/tutorial_contactForces.cpp.
#include <agxCollide/Contacts.h>
#include <agxCollide/Space.h>
// Return the sum of the magnitude for all contact forces being applied to a specific body.
agx::Real getContactForce(agx::RigidBody* body, agxCollide::Space* space)
{
// Get the vector with all the contacts
const agxCollide::GeometryContactPtrVector& contacts = space->getGeometryContacts();
agx::Real contactForce = 0;
// For all contacts in the system
for (size_t i = 0; i < contacts.size(); ++i)
{
agxCollide::GeometryContact *gc = contacts[i];
// Is the contact enabled?
if (!gc->isEnabled())
continue;
// Is our body involved in this contact?
if (gc->rigidBody(0) != body && gc->rigidBody(1) != body)
continue;
// Get all the points and sum the magnitude for the contact force (normal force)
const agxCollide::ContactPointVector& points = gc->points();
for (size_t n = 0; n < points.size(); ++n)
{
// Is the contact point enabled?
if (!points[n].enabled())
continue;
contactForce += points[n].getNormalForceMagnitude();
}
}
return contactForce;
}
// Build your simulation
// ...
// Create a body for which you want to read contact forces
agx::RigidBody *myRigidBody = new agx::RigidBody(new agxCollide::Geometry(new agxCollide::Sphere(0.3)));
simulation->add(myRigidBody);
simulation->stepForward();
agx::Real contactForce = getContactForce(myRigidBody, simulation->getSpace());
11.20.3.1. ContactForceReader
An alternative is to use the agx::ContactForceReader class. It has a simple interface and will perform the filtering and looping over contacts for you.
It can collect contact forces based on some interacting rigid bodies or geometries.
// Create a ContactForceReader object with a specific simulation.
agx::ContactForceReaderRef contactForceReader = new agx::ContactForceReader(simulation);
// Assume we have a simulation containing two rigid bodies (with geometries), ground and box:
agx::RigidBody* box = createARigidBodyBox();
agx::RigidBody* ground = createAGroundBody();
// Use a ContactForceReader to extract the sum of normal and frictional forces between two rigid bodies:
auto displayContactForces = [application](agxSDK::Simulation* , agx::ContactForceReaderRef contactForceReader, agx::RigidBody *ground, agx::RigidBody *box)
{
auto sceneDecorator = application->getSceneDecorator();
sceneDecorator->clearText();
sceneDecorator->setText(0, "Tutorial contact forces: ContactForceReader Friction force.");
// Get the total normal force between the two rigid bodies:
agx::Vec3 normalForce = contactForceReader->getNormalContactForces(ground, box);
// Get the total frictional force between the two rigid bodies
agx::Vec3 frictionForce = contactForceReader->getTangentialContactForces(ground, box);
sceneDecorator->setText(1, agx::String::format(" - Current normal force: %.10f N", normalForce.length()));
sceneDecorator->setText(2, agx::String::format(" - Current friction force: %.10f N", frictionForce.length()));
};
agxUtil::StepEventCallback::post(displayContactForces, simulation, contactForceReader, ground, box);
displayContactForces(simulation, contactForceReader, ground, box);
11.21. ObserverFrame
agx::ObserverFrame is a class that implements a coordinate transform that can be attached relative to a rigid body that will follow the movements of the body.
Given an observer frame the following data can be queried:
Position
Rotation
Linear/angular velocity
Linear/angular acceleration
Relative position, rotation, acceleration
This means that you can use an observer for measuring data in a system: What is the linear velocity on this point of a rigid body? The linear velocity will then be computed based on the rigid body’s linear and angular velocity. A typical scenario is to attach an observer to the chassie of a car to measure various data for the vehicle such as its position, heading, velocity etc.
Below is a code snippet illustrating the use of an ObserverFrame. There is also a python tutorial available: tutorial_observerFrame.agxPy.
// Create an observer that is attached to a specific RigidBody:
// It will get a name and a transformation relative to the attached rigidBody.
agx::ObserverFrameRef observer = new agx::ObserverFrame("MyObserver", rigidBody, agx::AffineMatrix4x4::translate(1, 0, 0));
// Add the observer to the simulation, only needed if you do not have a reference pointer to it, or
// if you want to find it later using: simulation->getObserver("MyObserver");
simulation->add(observer);
// Later in the simulation, after stepping, in an event listener etc. you can query the observer for data:
auto speed = observer->getVelocity().length();
// Simulate for 10 seconds
simulation->stepTo(10);
// Check if acceleration exceeds 9g -> damage to the person riding the car?
auto accelerationMagnitude = observer->getAcceleration().length();
if (accelerationMagnitude > 9 * agx::GRAVITY_ACCELERATION)
std::cerr << "Driver probably unconscious" << std::endl;